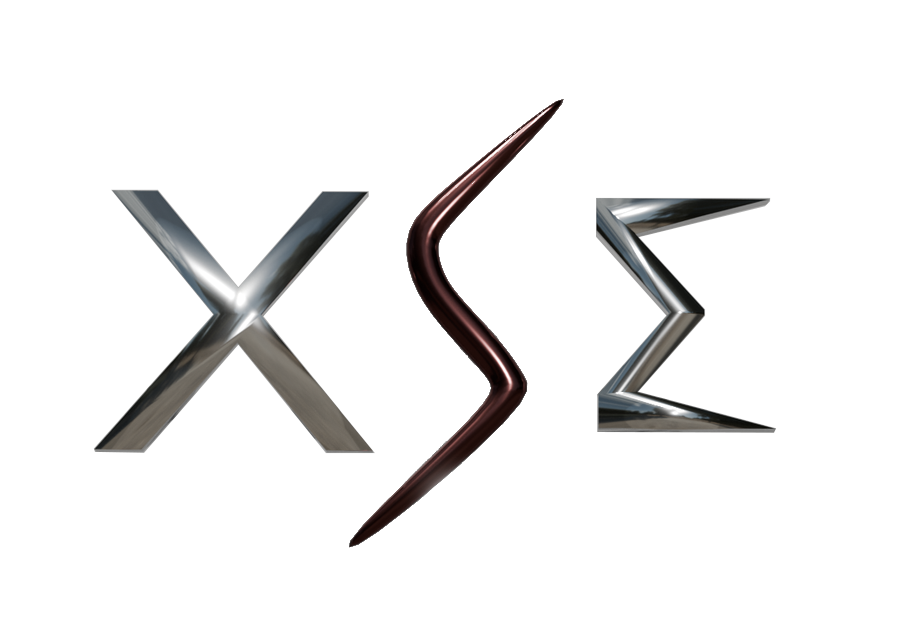Start at the beginning...

The foundation that mathematics and science were founded on thousands of years ago
In the nascent days of science, a profound intellectual revolution unfolded, marking the inception of axiomatic systems, Euclid’s Elements, the coordinate system, and the systematic application of logic. As ancient scholars grappled with understanding the natural world and formalizing mathematical principles, the introduction of axioms laid the groundwork for rigorous deductive reasoning. Euclid, in his seminal work “Elements,” meticulously organized geometric knowledge, providing a comprehensive and systematic foundation that became a cornerstone of mathematical thought for centuries. Concurrently, the development of coordinate systems brought forth a transformative means of representing spatial relationships, enabling mathematical descriptions of phenomena in both geometry and physics. The embrace of logical reasoning further elevated scientific discourse, fostering precision in argumentation and paving the way for the scientific method. In these formative stages, the convergence of axiomatic systems, Euclidean geometry, coordinate systems, and logical frameworks laid the groundwork for the scientific endeavors that would shape the course of human understanding for generations to come.
Axiomatic Fundamental Building Blocks

The plural of “axis” is “axes.” So, when referring to more than one axis, you would use the term “axes.” This applies in various contexts, such as mathematics, physics, and geometry, where the term is commonly used to describe lines or directions around which objects rotate or certain measurements are made.
For example:
- “The Cartesian coordinate system has three axes: x-axis, y-axis, and z-axis.”
- “The Earth rotates around its axis.”
- “To understand the movement of the object, consider both horizontal and vertical axes.”
In general, when discussing multiple instances of an axis, you would use “axes” to denote the plural form.
An axiom is a statement or proposition that is considered self-evidently true or accepted without needing proof. In various fields, including mathematics, logic, philosophy, and some branches of science, axioms serve as foundational principles or starting points upon which entire systems of thought or theories are built. Axioms are assumed to be true and are not derived from other statements or principles within the system.
Key characteristics of axioms include:
Self-Evidence or Intuitiveness: Axioms are typically regarded as self-evident or intuitively true. They are fundamental truths that are accepted without the need for further demonstration.
Foundational Role: Axioms play a foundational role in a particular system or theory. They serve as the basis for deriving other statements, theorems, or principles within that system.
Consistency: Axioms should be consistent within the logical framework they define. They should not lead to contradictions or inconsistencies when used to derive further conclusions.
Independence: Axioms are independent of one another within a given system. They are not derived from other axioms, forming a set of basic, irreducible assumptions.
Application in Different Fields: Axioms are used in various intellectual disciplines. In mathematics, for example, Euclidean geometry is built on a set of axioms. Similarly, foundational axioms exist in formal logic, set theory, and other branches of mathematics.
Examples of axioms in different contexts include:
- In Euclidean geometry, the parallel postulate is often considered an axiom.
- In set theory, the Zermelo-Fraenkel set theory includes axioms that define the basic properties of sets.
- In propositional logic, axioms might include statements like the law of identity (p → p).
Axioms are essential for constructing logical and consistent systems of thought, providing the starting point for reasoning and deduction within a particular framework.
Axiology is a branch of philosophy that deals with the study of values, including those related to ethics, aesthetics, and epistemology. Axiology explores questions about what is valuable, what constitutes goodness, and how individuals make judgments about the nature of things based on their intrinsic worth or importance.
There are two primary branches within axiology:
Ethics or Moral Axiology: Ethics, a subset of axiology, is concerned with the study of moral values and principles. It delves into questions about what is right or wrong, good or bad, and how individuals should behave in various situations. Different ethical theories, such as consequentialism, deontology, and virtue ethics, fall under the umbrella of moral axiology.
Aesthetics: Aesthetics, another branch of axiology, focuses on the study of values related to beauty, art, and sensory experiences. It explores questions about what is considered aesthetically pleasing, the nature of artistic expression, and the criteria for evaluating artistic works. Aesthetics seeks to understand subjective experiences of beauty and the principles that guide judgments in the realm of art and aesthetics.
Axiology addresses fundamental questions such as:
- What is the nature of value?
- How do we determine what is valuable or good?
- Are values objective, subjective, or a combination of both?
- How do different cultures and individuals perceive and prioritize values?
Philosophers who have contributed to the field of axiology include Friedrich Nietzsche, Max Scheler, and Robert S. Hartman, among others. Axiology plays a significant role in shaping ethical theories, guiding discussions on morality, and contributing to the understanding of aesthetics and the appreciation of beauty in various forms.
“[I]n logic, a procedure by which an entire system (e.g., a science) is generated in accordance with specified rules by logical deduction from certain basic propositions (axioms or postulates), which in turn are constructed from a few terms taken as primitive.”
Source: Britannica, The Editors of Encyclopaedia. “axiomatic method”. Encyclopedia Britannica, 26 Sep. 2011, https://www.britannica.com/science/axiomatic-method. Accessed 13 January 2024.
The axiomatic method is a systematic approach used in mathematics and philosophy to formulate and study mathematical and logical systems. It involves establishing a set of axioms, which are self-evident or intuitively true statements, and then using logical reasoning and deductive methods to derive theorems and explore the properties of the system.
Key features of the axiomatic method include:
Axioms as Starting Points: Axioms are assumed to be true without requiring proof within the context of the system. They serve as the foundational principles upon which the rest of the mathematical or logical structure is built.
Logical Deduction: The axiomatic method employs logical deduction to derive new statements (theorems) from the axioms. Logical rules of inference and rigorous reasoning are used to establish the validity of the derived results.
Systematic Development: The axiomatic method emphasizes a systematic and step-by-step development of mathematical or logical theories. Each statement or theorem is carefully derived from the axioms using well-defined rules of logic.
Precision and Clarity: Axiomatic systems aim for precision and clarity in their formulations. Clear definitions, explicit axioms, and rigorous reasoning contribute to the clarity and unambiguous nature of the system.
Consistency and Completeness: A primary goal of the axiomatic method is to ensure the consistency and completeness of the mathematical or logical system. Consistency means that the system does not lead to contradictions, and completeness implies that all logically valid statements within the system can be proven true or false.
Foundation for Mathematical Structures: The axiomatic method is foundational in the development of various branches of mathematics, such as geometry, set theory, and number theory. It provides a rigorous framework for exploring mathematical structures and relationships.
One of the most famous examples of the axiomatic method is Euclidean geometry, where Euclid formulated a set of axioms that became the foundation for classical geometry for many centuries.
The axiomatic method has been influential not only in mathematics but also in areas of philosophy, logic, and theoretical sciences. It contributes to the development of clear and rigorous theories, ensuring that mathematical and logical reasoning follows a well-defined and principled approach.
An axiomatic system, also known as a formal system or deductive system, is a structured set of axioms and rules that are used to build a logical framework for reasoning and deduction. This system provides a foundation for deriving theorems and making logical inferences within a specific domain of study, such as mathematics, logic, or philosophy.
Key components of an axiomatic system include:
Axioms: Axioms are self-evident or assumed statements that serve as the starting points of the system. They are accepted without proof within the context of the system and form the foundational principles upon which other statements are built.
Rules of Inference: Rules of inference are systematic procedures or logical rules that dictate how new statements or theorems can be derived from existing ones. These rules ensure that the deductive process remains consistent and valid within the system.
Logical Symbols and Notations: The system includes a set of logical symbols and notations that allow for the representation of statements, propositions, and logical relationships. These symbols help express the axioms, theorems, and logical connections within the system.
Definitions: Definitions may be included in the axiomatic system to specify the meanings of terms and concepts used within the system. Clear and precise definitions contribute to the clarity and rigor of the deductive reasoning process.
Theorems: Theorems are statements that can be proven true within the axiomatic system using the axioms and rules of inference. Theorems are derived logically from the axioms and previously established theorems.
Consistency and Completeness: An axiomatic system aims to be both consistent (free of contradictions) and complete (able to prove or disprove all logically valid statements within its scope). Achieving both consistency and completeness is a fundamental goal in the development of axiomatic systems.
Examples of well-known axiomatic systems include:
Euclidean Geometry: Based on a set of axioms, including the parallel postulate, this system forms the foundation for classical geometry.
Zermelo-Fraenkel Set Theory: A foundational axiomatic system in mathematics used to formalize the concept of sets.
Propositional Logic: An axiomatic system for reasoning about propositions, involving axioms and rules of inference.
Each axiomatic system is tailored to a specific domain of study, and the selection of axioms reflects the intended focus and goals of that system. The development and analysis of axiomatic systems are fundamental to the fields of mathematics, logic, and philosophy.
The term “axis” can have different meanings depending on the context in which it is used. Here are a few common definitions:
Geometry and Mathematics: In geometry, an axis is a straight line around which a geometric figure rotates or is symmetrically arranged. For example, in a Cartesian coordinate system, the x, y, and z axes are the three mutually perpendicular lines that define a three-dimensional space.
Anatomy: In anatomy, an axis often refers to the second cervical vertebra (C2), which is also known as the axis bone. It plays a crucial role in the rotation of the head.
Physics: In physics, the term axis is used to describe an imaginary line around which an object rotates. This concept is often used in the study of rotational motion.
Political Science: In political science, the term “axis” can be used to describe a political, military, or economic alliance between two or more countries. For example, during World War II, the alliance between Germany, Italy, and Japan was referred to as the Axis powers.
Statistics: In statistics, an axis refers to one of the lines on a graph, such as the x-axis or y-axis, used to represent variables and their relationships.
Psychology: In psychology, the term axis is sometimes used in the context of psychological assessment tools like the DSM-IV-TR (Diagnostic and Statistical Manual of Mental Disorders, Fourth Edition, Text Revision), where there are multiaxial assessments for clinical evaluation.
These are just a few examples, and the meaning of “axis” can vary depending on the field of study or application. It’s important to consider the specific context in which the term is used to determine its precise meaning.
Logic is the systematic study of the principles of valid inference and correct reasoning. It is a branch of philosophy and mathematics that explores the structure of arguments and the relationships between propositions. Logic provides a framework for analyzing and evaluating reasoning processes, helping to distinguish between valid and invalid forms of reasoning.
Key components and concepts in logic include:
Propositions: Logic deals with propositions, which are statements that can be either true or false. Propositions are the basic building blocks of logical reasoning.
Inference: Inference refers to the process of drawing conclusions based on given information or premises. Logical inference involves determining whether the conclusion follows logically from the premises.
Deductive Reasoning: Deductive reasoning involves deriving specific conclusions from general principles or premises. If the reasoning is valid and the premises are true, the conclusion must also be true.
Inductive Reasoning: Inductive reasoning involves making generalizations based on specific observations or evidence. Unlike deductive reasoning, inductive reasoning does not guarantee the truth of the conclusion.
Logical Connectives: Logical connectives, such as “and,” “or,” “not,” “if…then,” and “if and only if,” are used to combine propositions and form more complex statements.
Truth Tables: Truth tables are used to systematically represent the truth values of compound propositions for all possible combinations of truth values of their component propositions.
Formal Languages: Logic often employs formal languages with precise syntax and semantics to represent and analyze logical statements. Symbolic logic, including propositional logic and predicate logic, is commonly used in formalizing logical reasoning.
Fallacies: Fallacies are errors in reasoning that may lead to incorrect conclusions. The study of fallacies is an important aspect of logic as it helps identify and avoid common pitfalls in argumentation.
Modal Logic: Modal logic deals with modalities such as necessity and possibility. It extends classical logic to handle statements about necessity, contingency, and impossibility.
Philosophical Logic: In philosophy, logic is often used to explore fundamental questions about the nature of truth, knowledge, and existence. Philosophical logic extends beyond formal systems to address broader philosophical issues.
Logic plays a crucial role in various disciplines, including mathematics, computer science, linguistics, and philosophy. It provides a systematic and rigorous framework for evaluating the validity of arguments and reasoning processes.
The term “origin” can have different meanings depending on the context in which it is used. Here are a few common definitions:
Starting Point or Beginning: In a general sense, the origin refers to the starting point or beginning of something. For example, the origin of a journey is the place where it starts, and the origin of a river is its starting point.
Ancestry or Source: Origin can also refer to the point of ancestry or source from which something derives. For instance, a person’s origin might be their place of birth or the country from which their family comes.
Cause or Explanation: In the context of explanations or causes, origin can refer to the reason or cause behind something. For example, understanding the origin of a problem involves identifying its root cause.
Mathematics and Coordinates: In mathematics, particularly in the context of coordinate systems, the origin is the point where the axes intersect. In a Cartesian coordinate system, the origin has coordinates (0, 0).
Historical or Cultural Beginnings: Origin can refer to the historical or cultural beginnings of a particular idea, practice, tradition, or concept. For instance, the origin of a language, a tradition, or a custom may be traced back to a specific historical period.
In each of these contexts, “origin” is used to describe the point from which something comes into existence, starts, or is derived. The specific meaning is determined by the subject matter or the field in which the term is being used.
There are 7 of axioms used in Independent Integration Systems Engineering: The Alpha Axiom- “Integrity is founded on truth.” The First Axiom- “True and optimal intelligence is founded on integrity.” The Second Axiom- “True and optimal strength is founded on integrity.” The Third Axiom- “True and optimal freedom is founded on integrity.” The X Axiom- “Using critical and creative thinking sharpens the mind.” The Y Axiom- “The application of optimal choices strengthens the system.” The Z Axiom- “Seeking authentic and ultimate sources maximizes freedom.” These Axioms are used within the XSE Axiomatic Method as means for valuation, plotting, positioning, analysis, application and performance of X Systems Engineering within the XSE Axiomatic System. See The XSE Axiomatic System for more details.
The Axiomatic Method is a powerful tool for understanding and building complex mathematical theories...

The axiomatic method and axiomatic system are closely related concepts in mathematics.
The axiomatic method is a systematic approach to mathematical reasoning that relies on a set of fundamental principles, called axioms, from which all other mathematical statements and theorems are derived. These axioms are assumed to be true without requiring proof, and they serve as the foundation upon which the entire mathematical framework is built.
An axiomatic system, on the other hand, is a formal structure that consists of a set of axioms along with a set of rules of inference or logical rules that govern the derivation of new statements or theorems from these axioms. The axioms provide the starting point, and the rules of inference dictate how valid conclusions can be drawn from them.
...and has been incredibly successful in many areas of mathematics...

While Euclid is not typically considered the founder of the axiomatic method, he is highly influential in its historical development, particularly in the field of geometry. Euclid, a Greek mathematician who lived around 300 BCE, is best known for his work “Elements,” a comprehensive compilation of knowledge in geometry and number theory.
In “Elements,” Euclid presented a systematic approach to geometry based on a set of postulates (axioms), common notions, and definitions. His axiomatic approach involved stating a small set of foundational principles from which he deduced a large body of geometric knowledge through logical reasoning. Euclid’s work laid the groundwork for what later became known as the axiomatic method.
Key elements of Euclid’s axiomatic method in “Elements” include:
Axioms (Postulates): Euclid started with a set of axioms or postulates, self-evident statements that he assumed to be true without proof. These axioms formed the foundation for geometric reasoning.
Common Notions: Euclid introduced common notions, which were general truths that were universally accepted, such as “Things equal to the same thing are equal to each other.”
Definitions: Euclid provided clear and precise definitions for geometric terms, ensuring that readers understood the terms used in his system.
Logical Deduction: Euclid used deductive reasoning to derive theorems from the axioms and definitions. Each step in his proofs was based on previously established results.
While Euclid’s work primarily focused on geometry, his approach to formulating a systematic and deductive framework influenced the development of the axiomatic method in other areas of mathematics and philosophy. Later mathematicians and logicians built upon Euclid’s ideas, refining and extending the axiomatic method to various branches of mathematics and theoretical sciences.
Logic is the systematic study of the principles of valid inference and correct reasoning. It is a branch of philosophy and mathematics that explores the structure of arguments and the relationships between propositions. Logic provides a framework for analyzing and evaluating reasoning processes, helping to distinguish between valid and invalid forms of reasoning.
Key components and concepts in logic include:
Propositions: Logic deals with propositions, which are statements that can be either true or false. Propositions are the basic building blocks of logical reasoning.
Inference: Inference refers to the process of drawing conclusions based on given information or premises. Logical inference involves determining whether the conclusion follows logically from the premises.
Deductive Reasoning: Deductive reasoning involves deriving specific conclusions from general principles or premises. If the reasoning is valid and the premises are true, the conclusion must also be true.
Inductive Reasoning: Inductive reasoning involves making generalizations based on specific observations or evidence. Unlike deductive reasoning, inductive reasoning does not guarantee the truth of the conclusion.
Logical Connectives: Logical connectives, such as “and,” “or,” “not,” “if…then,” and “if and only if,” are used to combine propositions and form more complex statements.
Truth Tables: Truth tables are used to systematically represent the truth values of compound propositions for all possible combinations of truth values of their component propositions.
Formal Languages: Logic often employs formal languages with precise syntax and semantics to represent and analyze logical statements. Symbolic logic, including propositional logic and predicate logic, is commonly used in formalizing logical reasoning.
Fallacies: Fallacies are errors in reasoning that may lead to incorrect conclusions. The study of fallacies is an important aspect of logic as it helps identify and avoid common pitfalls in argumentation.
Modal Logic: Modal logic deals with modalities such as necessity and possibility. It extends classical logic to handle statements about necessity, contingency, and impossibility.
Philosophical Logic: In philosophy, logic is often used to explore fundamental questions about the nature of truth, knowledge, and existence. Philosophical logic extends beyond formal systems to address broader philosophical issues.
Logic plays a crucial role in various disciplines, including mathematics, computer science, linguistics, and philosophy. It provides a systematic and rigorous framework for evaluating the validity of arguments and reasoning processes.
Logic is indeed fundamental to a wide range of disciplines and is often considered a foundational aspect of rational inquiry. While its explicit application and prominence may vary across disciplines, the principles of logic underpin the processes of reasoning, argumentation, and analysis in many areas of study. Here are several disciplines where logic plays a crucial role:
Philosophy: Logic is a central component of philosophy, where it is used to analyze arguments, assess the validity of reasoning, and explore fundamental concepts such as truth and knowledge.
Mathematics: Mathematics relies heavily on logical reasoning, especially in areas such as proof theory, mathematical logic, and formal systems. Axiomatic methods and logical structures are foundational to mathematical thinking.
Computer Science: Logic is essential in computer science for designing algorithms, programming languages, and systems. Formal logic, including propositional and predicate logic, is applied in areas such as artificial intelligence, database design, and software verification.
Science: Logical reasoning is integral to the scientific method. Hypotheses are formulated logically, experiments are designed to test them, and conclusions are drawn based on deductive and inductive reasoning.
Linguistics: Logic is used in linguistic analysis to study the structure and meaning of language. Formal logic and semantics help linguists analyze and represent the logical relationships within sentences.
Law: Legal reasoning involves the application of logical principles to interpret laws, construct arguments, and make legal decisions. Logical consistency and coherence are crucial in legal argumentation.
Philosophy of Science: The philosophy of science often involves logical analysis, examining the structure of scientific theories, the nature of scientific explanation, and the logic of scientific inference.
Critical Thinking: Logic is a cornerstone of critical thinking, a skill applicable across disciplines. Critical thinking involves assessing arguments, identifying fallacies, and making well-reasoned judgments.
Ethics: Ethical reasoning often relies on logical analysis to evaluate moral principles and arguments. Logical consistency is crucial in ethical deliberation.
Cognitive Science: In the study of cognition, logic is employed to understand reasoning processes, decision-making, and problem-solving strategies in the human mind.
While not every discipline explicitly formalizes logic, its principles are pervasive in shaping the methods of inquiry and reasoning within those disciplines. Whether uncovering mathematical truths, formulating scientific hypotheses, or constructing persuasive arguments, logical principles are at the core of intellectual pursuits across various fields.
The axiomatic method has been foundational in the development of modern mathematics, leading to numerous breakthroughs and advancements across various branches of the discipline. Some of the key mathematical breakthroughs that have been influenced or facilitated by the axiomatic method include:
Non-Euclidean Geometry: The discovery of non-Euclidean geometries by mathematicians such as Nikolai Lobachevsky, János Bolyai, and Carl Friedrich Gauss challenged the assumptions of Euclidean geometry. The axiomatic method allowed for the exploration and formalization of alternative geometries, contributing to the understanding of curved spaces.
Set Theory: Georg Cantor’s development of set theory in the late 19th century is a significant breakthrough influenced by the axiomatic method. Cantor formulated the foundational principles of set theory, which played a crucial role in understanding the nature of infinity and continuum.
Foundations of Mathematics: David Hilbert’s formalization of the axiomatic method and his efforts to create a consistent and complete set of axioms for all of mathematics had a profound impact. The work of logicians such as Kurt Gödel and his incompleteness theorems, which showed the inherent limitations of formal axiomatic systems, also emerged within this context.
Abstract Algebra: The development of abstract algebra, including group theory, ring theory, and field theory, was greatly influenced by the axiomatic method. Mathematicians like Évariste Galois and David Hilbert contributed to the formalization and generalization of algebraic structures based on axioms.
Mathematical Logic: Mathematical logic, particularly the work of logicians such as Alfred North Whitehead and Bertrand Russell (in their “Principia Mathematica”) and Kurt Gödel, involves the application of the axiomatic method to the study of formal systems and the nature of mathematical reasoning.
Topology: The axiomatic method has been instrumental in the development of topology, where the concept of open sets and other fundamental ideas are defined axiomatically. This branch of mathematics explores properties preserved under continuous deformations, and axioms help formalize these concepts.
Category Theory: Category theory, a modern branch of mathematics introduced by Samuel Eilenberg and Saunders Mac Lane in the mid-20th century, uses an axiomatic approach to study abstract structures and relationships between them. It provides a unified framework for understanding diverse mathematical concepts.
The axiomatic method has been a powerful tool in clarifying and formalizing mathematical theories, fostering rigorous reasoning, and facilitating communication within the mathematical community. Many mathematical breakthroughs and advancements owe their clarity and depth to the axiomatic method’s influence on the development of mathematical structures and theories.
...from teachings based on logic to rocket science.

Imagine what many people may have said to Euclid about his passionate pursuit of understanding and developing the field of mathematics. A big question that he probably was frequently faced with was “why? what’s the point?” Even today, it seems that many students begrudgingly tolerate math classes with no understanding of what the purpose is in the big picture. If Euclid could have seen into the future he would have understood that what he was developing as a discipline would eventually lead to the specific numerical expressions of physics, eventually developing into the modern technology that we know today, from our cell phones to the aerospace industry. Logic is the foundation for math. Math is the foundation for physics. Thank you Euclid for not letting the nay-sayers get to you.
Coordinate Systems

An axiomatic coordinate system refers to a mathematical framework used to represent spatial relationships and positions based on a set of fundamental axioms or postulates. Axioms are self-evident truths or principles that serve as the foundation for the system, guiding the derivation of theorems and ensuring the logical consistency of the coordinate system.
Key characteristics of an axiomatic coordinate system include:
Axioms: The system is built upon a set of axioms that establish basic truths about points, lines, distances, and other geometric entities within the coordinate space. These axioms provide the fundamental rules governing the behavior of the system.
Coordinates: The system assigns numerical values, known as coordinates, to points within the coordinate space. These coordinates are often represented as ordered tuples or vectors, depending on the dimensionality of the space.
Measurement: The axioms define the rules for measuring distances, angles, and other geometric properties within the coordinate system. This measurement process adheres to the principles established by the axioms.
Logical Consistency: The axioms ensure the logical consistency of the coordinate system, providing a solid and coherent foundation for geometric reasoning and mathematical operations.
Derivation of Theorems: The axioms serve as starting points for the derivation of theorems and mathematical propositions within the system. Theorems are logical consequences of the axioms and contribute to the understanding of spatial relationships.
Applicability: Axiomatic coordinate systems can be applied in various mathematical and scientific contexts, including geometry, physics, engineering, and computer science. They provide a rigorous and systematic framework for representing and analyzing spatial structures.
Extension to Different Dimensions: Axiomatic coordinate systems can be designed for two-dimensional (2D), three-dimensional (3D), or even higher-dimensional spaces, depending on the specific requirements of the application.
The development of an axiomatic coordinate system involves carefully selecting axioms that capture essential geometric truths and ensuring that they form a consistent and complete set. A well-defined axiomatic system contributes to the clarity and precision of mathematical reasoning within the coordinate space.
An epoch-based coordinate system is a celestial coordinate system that is referenced to a specific epoch, which is a particular moment in time. The term “epoch” is used to denote the reference date to which the coordinates of celestial objects are tied. The choice of epoch is significant because the positions of celestial objects change over time due to factors such as the Earth’s precession, nutation, and the motion of celestial bodies.
Two common epoch-based coordinate systems used in astronomy are the Besselian Epoch and the Julian Epoch. Additionally, the B1950.0 and J2000.0 coordinate systems are widely used in modern astronomy.
Besselian Epoch (B): The Besselian Epoch is a coordinate system that uses the Besselian year as the unit of time. One Besselian year corresponds to the tropical year at a specific epoch. Coordinates referenced to the Besselian Epoch are often labeled with a “B” followed by the year, such as B1950.0.
Julian Epoch (J): The Julian Epoch is another epoch-based coordinate system that uses Julian years as the unit of time. One Julian year corresponds to the Julian calendar year. Coordinates referenced to the Julian Epoch are often labeled with a “J” followed by the year, such as J2000.0.
B1950.0 and J2000.0 Coordinate Systems: These coordinate systems are commonly used in modern astronomy. B1950.0 refers to coordinates referenced to the Besselian Epoch at the beginning of the year 1950, and J2000.0 refers to coordinates referenced to the Julian Epoch at the beginning of the year 2000.
Epoch-based coordinate systems are essential in providing a stable reference frame for celestial objects over extended periods. They allow astronomers to specify the positions and motions of celestial objects with respect to a fixed reference frame, making it easier to compare observations made at different times. When using epoch-based coordinates, it’s important to account for the proper motions and precession of celestial objects over time to ensure accurate and up-to-date positional information.
A coordinate system is a mathematical framework used to represent and locate points in space or on a plane. It provides a systematic way of assigning numerical values or coordinates to points, allowing for the precise description of positions and relationships between objects. Coordinate systems are widely used in various fields, including mathematics, physics, engineering, geography, and computer science.
Key components of a coordinate system include:
Coordinate Axes: The coordinate system typically consists of two or more axes (lines) that intersect at a reference point, called the origin. In a two-dimensional system, there are two axes (commonly labeled x and y), and in a three-dimensional system, there are three axes (x, y, and z).
Coordinates: Coordinates are numerical values assigned to points in the system. In a two-dimensional Cartesian coordinate system, a point is represented by an ordered pair (x, y), where x is the distance along the horizontal axis, and y is the distance along the vertical axis. In three dimensions, coordinates are represented as an ordered triplet (x, y, z).
Reference Point (Origin): The origin is the point where the coordinate axes intersect. It serves as the reference point from which distances are measured.
Quadrants (for 2D Systems): In two-dimensional Cartesian coordinate systems, the plane is divided into four quadrants based on the signs of the coordinates. The positive x-axis and positive y-axis define the positive directions in each quadrant.
Coordinate systems play a crucial role in mathematical modeling, problem-solving, and the representation of spatial relationships. Different types of coordinate systems exist, including Cartesian coordinates, polar coordinates, cylindrical coordinates, and spherical coordinates, each with its specific rules and applications. The choice of a coordinate system depends on the nature of the problem being addressed and the convenience of representation in a particular context.
There are several types of coordinate systems used in various fields, each designed to address specific needs and applications. Here are some common types of coordinate systems:
Cartesian Coordinate System: The most familiar and widely used coordinate system, consisting of two or three perpendicular axes (x, y, and sometimes z) intersecting at a point called the origin. Points are represented by ordered pairs or triplets of numerical values.
Polar Coordinate System: Represents points based on their distance from a central point (origin) and the angle formed by a ray extending from the origin to the point. Coordinates are often given in the form (r, θ), where r is the radial distance, and θ is the angle.
Cylindrical Coordinate System: Extends the polar coordinate system into three dimensions by adding a height (z) coordinate. Points are represented as (r, θ, z), where r is the radial distance, θ is the angle, and z is the height.
Spherical Coordinate System: Represents points using radial distance (r), polar angle (θ), and azimuthal angle (ϕ). It is well-suited for spherical objects. Coordinates are given as (r, θ, ϕ).
Homogeneous Coordinates: Used in computer graphics and computer vision, homogeneous coordinates extend Cartesian coordinates by adding an additional coordinate, often represented as w. This system simplifies certain transformations.
Geographic Coordinate System: Used to specify locations on the Earth’s surface. Points are represented by latitude and longitude coordinates.
Curvilinear Coordinates: Systems tailored to specific curved surfaces. Examples include curvilinear coordinates on surfaces like spheres or cylinders.
Body-Fixed Coordinates: Used in astronomy and aerospace, where coordinates are defined relative to the orientation of a celestial body or spacecraft.
Barycentric Coordinates: Used in geometry to represent points in terms of the masses of the vertices of a simplex (a generalization of a triangle or tetrahedron).
These are just a few examples, and many other coordinate systems exist, each designed for specific mathematical, scientific, or engineering applications. The choice of a coordinate system depends on the nature of the problem being addressed and the convenience of representation in a particular context.
Combining an axiomatic coordinate system with an epoch-based coordinate system involves incorporating both foundational principles (axioms) and a reference point in time (epoch) into a unified framework. Let’s explore how these elements can be integrated:
Axiomatic Coordinate System:
The axiomatic part establishes the foundational rules and principles governing the coordinate system. Axioms are self-evident truths or postulates that serve as the basis for deriving theorems and ensuring logical consistency within the system.
Axioms for a coordinate system might include statements about the existence of points, lines, and distances, as well as rules for measurement, transformations, and relationships between geometric entities.
Epoch-Based Coordinate System:
The epoch-based component introduces a reference point in time (epoch) within the coordinate system. This reference point is used to measure and express time-related coordinates or intervals.
The epoch may represent a significant event, a starting point for time measurements, or a reference moment for synchronization. Time coordinates could be expressed relative to this epoch, allowing for accurate temporal positioning.
Integration:
The integration of these two elements involves incorporating the axiomatic principles with the epoch-based time dimension. This integration ensures that both spatial and temporal aspects are systematically governed within the coordinate system.
The axioms guide the spatial relationships and measurements, while the epoch establishes a point in time for reference and synchronization. Together, they form a unified system capable of representing not only spatial positions but also time-related information.
Applications:
Such a combined system could find applications in various fields, including astronomy, navigation, and dynamic systems modeling. For instance, in celestial mechanics, the axiomatic principles govern the spatial relationships of celestial bodies, while the epoch-based component allows for precise temporal positioning of events or observations.
In navigation, the integration could be valuable for tracking the position of objects over time, considering both spatial coordinates and the chronological context.
This integration allows for a comprehensive approach where the axioms establish the foundational rules for spatial relationships, and the epoch adds a temporal dimension to the coordinate system, making it suitable for applications that involve both space and time considerations.
XSE integrates the Axiomatic coordinate system with an Epoch-based coordinate system to achieve an
Epoch-Axiomatic Coordinate System
Such a combined system could find applications in various fields, including astronomy, navigation, and dynamic systems modeling. For instance, in celestial mechanics, the axiomatic principles govern the spatial relationships of celestial bodies, while the epoch-based component allows for precise temporal positioning of events or observations. In navigation, the integration could be valuable for tracking the position of objects over time, considering both spatial coordinates and the chronological context.
This integration allows for a comprehensive approach where the axioms establish the foundational rules for spatial relationships, and the epoch adds a temporal dimension to the coordinate system, making it suitable for applications that involve both space and time considerations.
The "Timeless Timeline" of XSE's Y Axis is Intriguingly Epic


XSE considers the actual stage of the system as being more relevant than the chronological age measured in months or years. This is due to the fact that a 50 year-old system that has undergone excellent maintenance and continual optimization and upgrades will most likely be in a better state of “system health” than the same kind of system only 30 years old that has been through “hell” without any care or system maintenance, optimization or upgrades. Today, more than ever, with the wide variety of what can be applied and input in a system, chronological time can be less of a factor in the actual stage of the systems life cycle than the time it has been in existence. Plot the life cycle stages that are appropriate and fitting for your SOI on the positive side of the Y axis. The negative side of the Y axis is reserved for any application to the system that contributes to system breakdown or failure.
One of the infinite applications of math manifest: